In convertible arbitrage, traders rely on models to determine the fair value of the convertible bond. There are only a few variables that determine the value of the converts. These are underlying stock price, volatility of the underlying stock, credit spread, risk free rate, time to put/maturity, and dividend of the underlying stock. Each of these variables have greeks associated with that measures the rate of change of the convertible fair value (CFV) for each unit move of the variable.
- Delta (Δ) = change in CFV per unit change in underlying stock price
- Vega (v) = change in CFV for a 1% change in the underlying stock’s implied volatility
- Theta (Θ) = change in CFV for a 1 day change in the number of days to expiry
- Rho (ρ) = change in CFV for a 10 bps change in interest rates
- Omnicron (ο) = change in CFV for a 10 bps change in credit spread
- Phi (Φ) = change in CFV with respect to the underlying stock dividend yield
and finally,
- Gamma (Γ) = the second derivative of CFV with respect to change in underlying stock price.
Many of the concepts here were taken from the book, Convertible Aribitrage by Nick Calamos (2003), a highly recommended book for those interested in convertible arbitrage.
Delta
Delta measures the change in the convertible’s price with respect to the change in the underlying common stock price. The delta measures the convertible equity’s sensitivity for very small stock-price changes. In a convertible arbitrage position, the trader will own the convertible bond and short an amount of stock that is equal to the delta of the convertible bond.
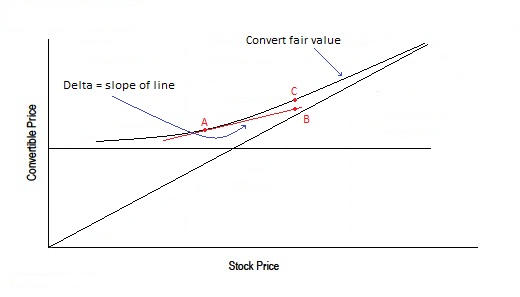
The graph below show a visualization of a convertible’s delta. The delta is the slope of the line that is tangent to the convertible’s fair value line at a particular stock price. A convertible bond has a particular delta at point A. A convert that is hedged on that delta will move to point B as the stock moves up. Since point B is below the convert’s fair value line, the convert price will then appreciate in price to point C in an efficient world.
For a typical convertible bond, delta increases as the underlying stock price increases and approaches 1.0 as the convertible moves deep in the money. The price of a convertible that is deep in the money will see a percentage change very close to the price of the underlying stock.
On the other end of the spectrum, delta will approach 0 as the convertible moves out of the money. The price of an out of the money convertible will behave like fixed income and only change at a fraction of the change in the underlying stock price.
Gamma
Gamma is the second-order partial derivative of the convertible’s price with respect to changes in the underlying stock. Gamma is also the change in delta with respect to the change in the underlying stock price. Gamma is highest with the underlying stock price at the conversion price. At that point, the delta of the convertible changes the most rapidly. Convertibles that are deep in the money or out of the money have low gammas.
Gamma is also higher for shorter dated converts all else being equal.
With a convertible arbitrage position hedged at a specific delta, positive gamma means the price of the convert will increase more than the short stock position on the way up and decrease less than the short stock position on the way down.
Traders can “capture” this gamma by re-hedging to the new delta when the stock moves.
Typically, traders will re-hedge for every 1% move in stock price. In the best scenario, a stock will gap up or down by more than 10%, thus allowing a significant amount of gamma capture.
Vega
Vega measures the change in the convertible’s price to changes in implied volatility. Increases in volatility raises the value of a convertible while decreases in volatility lowers the value of a convertible.
Traders will own a convertible position where the implied volatility is below its expected volatility. Traders will hold the position until the implied volatility rebounds to the level that they expect. The vega risk measure quickly indicates the upside capture from a move in the volatility back to the expected volatility level or the reverse.
The vega curve is similar to the gamma curve in that convertibles in the money or out of the money demonstrate lower vegas.
The best way to visualize vega is that a convertible with a higher vega has a fair value curve that is higher than a convert with a lower vega, all else being equal.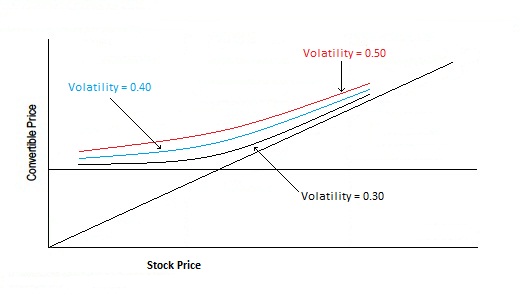 Theta
Theta
Theta measures the change in the convertible’s price with respect to changes in time. The time premium decay of a convertible is complicated to some degree by the realization that the option portion of the convertible is subject not only to a maturity date but also to variations in call probabilities. Like an option, convertibles nearing maturity or the end of their call protection trade with a higher degree of theta risk. Unlike an option, a convertible that is slightly out of the money with no call protection remaining but with a low coupon payment on the issue will most likely remain outstanding. However, a reduction in interest rates to levels that may make the convertible issuer likely to call the issue in order to refinance at a lower rate has the effect of increasing the theta risk of the issue.
To visualize theta, picture convertible fair value curves declining as time passes.

Rho
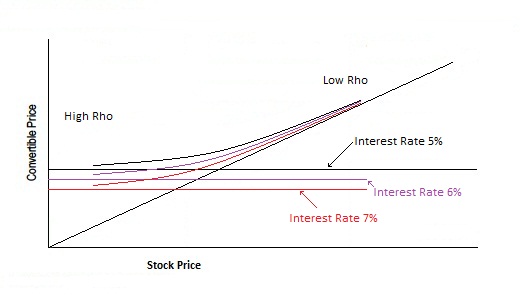
Rho measures the change in the convertible’s price with respect to a change in interest rates. Higher interest rates result in lower convertible values. Convertibles will have a different interest rate sensitivity than straight bonds because the option component of the convertible moves in tandem with rate changes, slightly offsetting the interest rates impact on the convertible. Convertibles have negative rho at most points along the convertible price track. The negative rho exists because as interest rates increase, the investment value decreases. A deep in the money convert will exhibit a rho near zero.
To visualize Rho, imagine the entire convert fair value curve shifting down as interest rates increase. As you can see, the convertible fair value has the greatest change when the convert is deep out of the money and the smallest change when the covert is deep in the money.
Omnicron
Omnicron measures the change in the convertible’s price with respect to the change in credit spread. An out of the money convertible is generally more sensitive to changes in credit spreads than any other variable. In general, as credit spreads narrow, a convertible’s value increases and as spreads widen, the convertible’s value decreases.
Convertibles that are deep in the money have a very low sensitivity to credit spread changes. Omnicron is one of the most important risk measures for convertible arbitrageurs hedging low-grade issues that are trading near or below their exercise price.
Upsilon
Upsilon measures the change in the convertible’s price with respect to a change in the credit recovery rate. The credit recovery rate is an estimation of the principal amount recovered in the event of default on the security. Recovery rates depend on many factors including the seniority of claims on the borrower’s assets and the quality of the collateral.
As the stock price declines, the convertible bond becomes distressed and trades near recovery value, as investors see a high risk of bankruptcy. Upsilson becomes very high as the convert trades on expected recovery value.
Phi
Phi measures the change in the convertible’s price with respect to a change in the underlying stock dividend. A convertible’s fair value moves inversely to changes in the underlying stock dividend. The valuation of any convertible considers the present value of the convertible’s income minus the present value of the underlying stock dividend over the expected life of the security. The option value decreases with higher dividend yields because the option buyer does not receive the dividends.